R: Datenanalyse - Lokale Maxima finden

R ist eine Art Schweizer Messer für die Datenanlayse und Aufbereitung. Zusammen mit den Tidyverse Paketen schaffe ich es es in etwa 90% meiner Analysen abzudecken. Was oft noch dazu kommt sind Datenbankzugriff und Umformung von Datentabellen, das ersetze ich so langsam aber sicher durch tidyr. Für die Datenanalyse im Zuge meiner Dissertation bin ich auf das folgende interessante kleine Problem gestoßen. Ich will Daten, die geplottet das Bild unten ergeben, auswerten. Mich interessiert zu welchen Zeitpunkten im Siganl ein lokaler Hochpunkt auftritt.

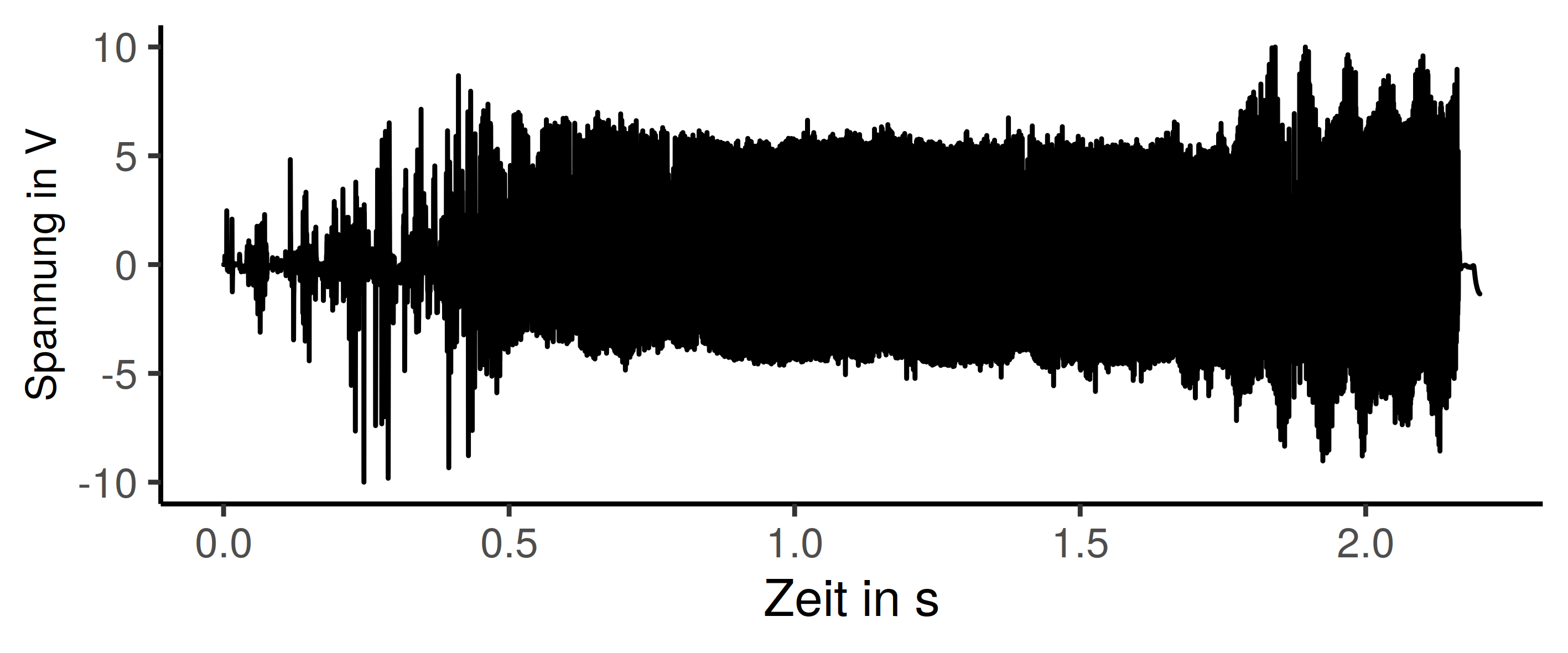
Das Plot ist in einer vollen Länge eher unhandlich und unübersichtlich. Zoomen wir also etwas hinein, dann werden die gesuchten lokalen Hochpunkte besser erkennbar. Das Ganze ist in etwa sinusförmig, das ist aufgrund der gemachten Messung auch erwartet. Der Anfangs des Datensatzes ist der Prozessstart und damit weniger gleichförmig. Sobald das läuft wie es soll, sollten in etwa die gezeigten Daten herauskommen. (Spoiler: Die gesuchten Punkte sind im Plot markiert, das Problem ist also mit Sicherheit lösbar)

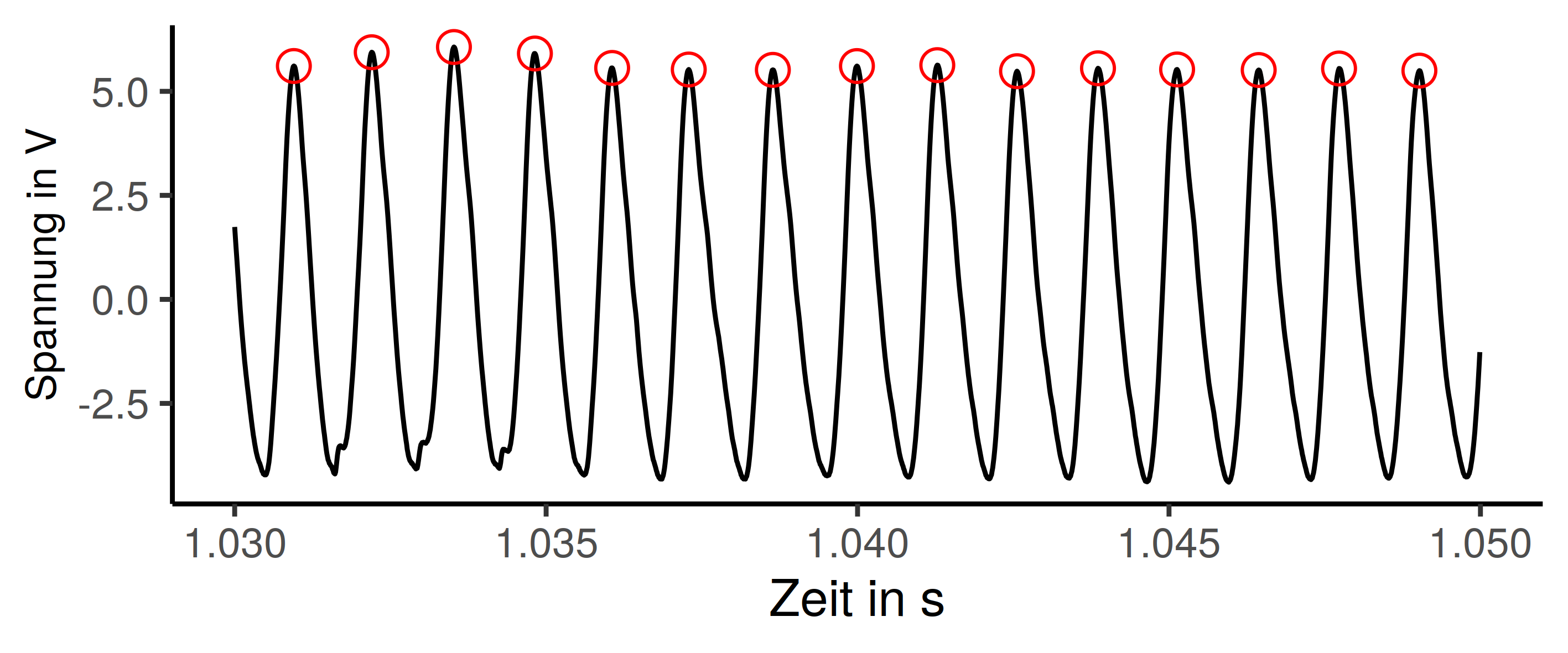
Das Problem ist mit dem Programmiergrundlagen aus dem Studium natürlich irgendwie lösbar. Das wird aber wahrscheinlich ein unschönes Schleifenkonstrukt mit gleitendem Mittelwert und if-Anweisungen, also nicht sehr im Stil von R. Als Nächstes gibt es die Möglichkeit ein Paket zu suchen, das die Aufgabe erledigt. Das ist schon mehr R-Stil, erhöht aber die Anzahl der Abhängigkeiten und nimmt die Freude am Selbermachen und damit auch die Chance etwas zu lernen.

Ich scheue immer etwas davor zurück eine neue Paketabhängigkeit zu schaffen. Ich muss mich in das Paket einarbeiten und es richtig anwenden. Mit etwas Pech stelle ich später fest, dass das Paket die Analyse die ich haben möchte doch nicht in der Form kann, die ich brauche.

Ran an die Daten

Meine Rohdaten sind in der Form:

> print(tdata, n=5)
# A tibble: 350,000 x 2
  messzeit      signal
     <dbl>       <dbl>
1  0        0         
2  0.00001  0         
3  0.00002  0         
4  0.00003 -0.00122070
5  0.00004  0.00122070
# … with 349,995 more rows     

Die Messzeit ist eine Gleitkommazahl, das Signal ist der skalierte Wert aus dem AD-Wandler der Messkarte. Der Zeitpunkt und y-Wert der Hochpunkte fällt aus diesem Anweisungsblock als Ergebnistabelle raus:

  thres <- 2
  tdata
  %>% mutate(valley = if_else(signal > thres, 0, 1))
  %>% mutate(grpsel = cumsum(valley))
  %>% mutate(peakgrp = if_else(valley == 0 , grpsel, 0))
  %>% filter(peakgrp > 0)
  %>% group_by(peakgrp)
  %>% summarise(t_hpt = messzeit[which.max(signal)], wert=max(signal))
  %>% ungroup()
  %>% select(-peakgrp)

und sieht so aus:

# A tibble: 1,569 x 2
    t_hpt   signal
     <dbl>   <dbl>
 1 0.00553 2.47437
 2 0.0147  2.08862
 3 0.07179 2.29980
 4 0.11683 4.82544
 5 0.13933 2.42920
 6 0.14211 3.12378
 7 0.14422 3.32764
 8 0.1938  2.90283
 9 0.19629 2.53052
10 0.20898 3.46924
# … with 1,559 more rows

Stellt sich noch die Frage: “Warum geht das?”

Das Ganze ist eine kreative Nutzung der Funktionen aus dem tidyverse, der %>% Operator nimmt das was links von ihm steht und verarbeitet das mir er Anweisung rechts, das kann man beliebig aneinander reihen. Die Einzelschritte lassen sich sogar im Plot mit darstellen.

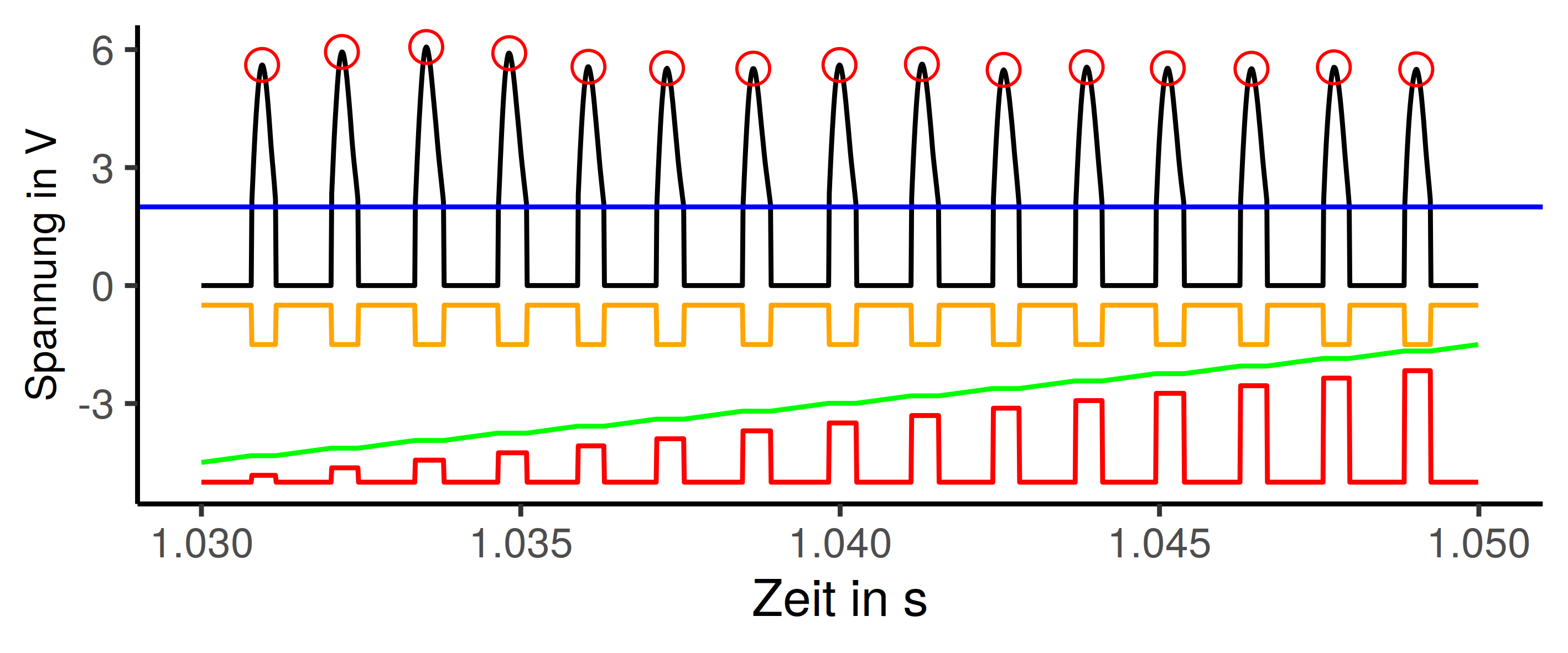
Zeilenweise Betrachtung:

• thres <- 2 legt die Variable für einen Grenzwert mit dem Wert 2 an. Blaue Linie im Plot.
• tdata steht links vom %>% stellt somit die Ausgangsdaten zur Verfügung
• %>% mutate(valley = if_else(signal > thres, 0, 1)) fügt eine neue Spalte in den Datensatz ein, 1 wenn die Werte unterhalb von thres liegen, 0 wenn sie darüber liegen Das entspricht dann der orangen Linie. Der Wert thres ist dazu da die lokalen Maxima zu trennen. Es werden nur die positven Halbwellen betrachtet, das entspricht der schwarzen Line.
• %>% mutate(grpsel = cumsum(valley)) legt eine neue Spalte mit den kummulierten Summe der Spalte valley an. Grüne Linie im Diagramm. Die hat die Eigenschaft, dass die Werte bei im Bereich von lokalen Hochpunkten konstant bleiben, sonst aber kontinuierlich steigen.
• %>% mutate(peakgrp = if_else(valley == 0 , grpsel, 0)) erzeut die dritte und letzte Hilfsspalte (rote Linie). Die Bereich von peakgrp mit konstanten Werten werden erhalten, die anderen auf 0 gesetzt. Jetzt hat jeder Datenbereich um ein lokals Maximum einen einzigartigen Wert in peakgrp zugeordnet.
• %>% filter(peakgrp > 0) entfernt alle Datenzeilen mit peakgrp == 0. Das sind alle Zeilen die nicht zu einem lokalen Maximum gehören.
• %>% group_by(peakgrp) sorgt dafür das für Befehle wie mutate(), filter(), summarise(), gruppenweise vorgeganen wird. Alle Zeilen die in peakgrp den gleichen Wert haben werden als eine Gruppe behandelt.
• %>% summarise(t_hpt = messzeit[which.max(signal)], wert=max(signal)) macht nach der ganzen Vorbereitung jetzt die Arbeit und fischt für jede Gruppe die Zeit des ersten Auftretens des jeweiligen Maximalwertes und den dazugehörgen Wert aus dem Signal.
• %>% ungroup() entfernt die Gruppierung wieder von den Daten, sonst macht das evtl. in weiteren Analysen Probleme
• %>% select(-peakgrp) löscht die Spalte peakgrp

Mit etwas “Out of the Box”-Denken lassen sie viele Probleme mit bekannten Mitteln und ohne neue Pakte/Bibliotheken lösen. Das schöne am Programmieren und Datenanalyse ist, das eine kreative Lösungssuche wirklich Spaß machen kann.